Array operation analysis

In this section, we’ll take a look at the three core operations on arrays:

1. accessing at item at a given index
2. adding an item at a given index
3. removing an item from a given index

NOTE: Time complexity analysis will be limited to HD-level questions in the final exam.

Accessing an item at a given index

We need to understand how an array is stored to understand how array items are accessed.

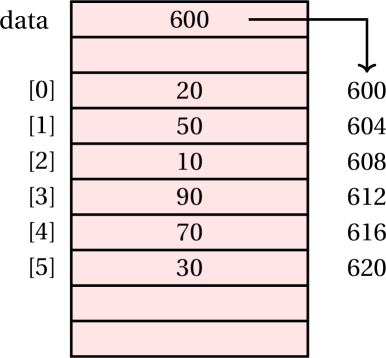
An array is stored as a contiguous block of memory.

As an example, if there is an array of 6 integers, 24 bytes are reserved (4 per integer). The first item is stored in the first four bytes, the second item in the next four bytes and so on.

Thus,

• The address of the first item (at index 0) is the base address of the array (in this example, 600).
• The address of the second item (at index 1) is the base address of the array + 4 bytes.
• The address of the third item (at index 2) is the base address of the array + 2 * 4 bytes.
• …

• The address of the last item (at index 5) is:

  base address of the array + 5 * 4 bytes.

With a little tweak we can see:

• Address(data[0]) = baseAddress + 0 * 4
• Address(data[1]) = baseAddress + 1 * 4
• Address(data[2]) = baseAddress + 2 * 4
• …
• Address(data[data.length - 1]) = baseAddress + (data.length - 1) * 4

Putting it all together,

(address of item at index idx) = (base address of array) + (size of each item) * (idx);

Example: Accessing an item

Let’s say we want to access data[3] in the following statement:

1
int item = data[3];

We start off with the reference held by data and getting the base address (600).

To that, we add 3 * 4 = 12 (3 being the index and 4 being size of each item), giving us the starting address of the item 612.

We grab 4 bytes starting at that address (so bytes 612 to 615) and present it packed as an integer: 90.

Inserting an item at a given index

There are four cases for inserting an item:

1. Array is not full and you are inserting an item at the end of the array: None of items need to be moved, array doesn’t need to be grown.

2. Array is full and you are inserting an item at the end of the array: None of items need to be moved but array needs to be grown. Growing the array is O(n). Therefore, time complexity in this case is O(n).

3. Array is not full but you are inserting an item somewhere (not at the end): Some items need to be moved but array doesn’t need to be grown. The worst case is when you are adding an item at index 0, in which case all items need to move, which is O(n). Therefore, time complexity in this case is also O(n).

   For example, if there are 5 items currently being used in an array of size 8, and we try to insert an item 5.6 at index 0, all 5 items need to be moved forward.

    

   

    

   These shifts are illustrated in the following diagram:

    

   

    

4. Array is full and you are inserting an item somewhere (not at the end): Double whammy, but O(n) + O(n) is still O(n).

Removing at item at a given index

There are two relevant cases for removing an item:

1. Removing the last item: No items need to be moved. O(1).

2. Removing the first item: All the items need to be moved. O(n).

   For example, if there are 5 items currently being used in an array of size 8, and we try to remove the first item, all 5 items need to be moved backward by one.

    

   

    

   These shifts are illustrated in the following diagram:

    

   

    

Homework exercises

1. Explain the calculations performed during calculating the address of data[6] if the base address is 4000 and the array is of type double[]. Each double variable needs 8 bytes of memory.

2. Explain the calculations performed during calculating the address of data[40] if the base address is 3000 and the array is of type char[]. Each char variable needs 2 bytes of memory.

3. Consider an array data = {10, 70, 20, 90, 30, 80, 60}. Explain, with the help of a diagram, the shifts involved while removing the item 70.

4. Consider an array data = {10, 70, 20, 90, 30, 80, 60}. Explain, with the help of a diagram, the shifts involved during the process of adding the item 30 at index 1.